Deep Into Denoising Diffusion Probabilistic Models (DDPM)
生成式模型
- Normalizing Flows
- GANs
- VAEs
- . . .
他们的核心思想都是将来自简单分布的噪声转换为数据样本,DDPM 也正是如此,它从纯噪声开始学习并逐渐对数据进行去噪;
DDPM
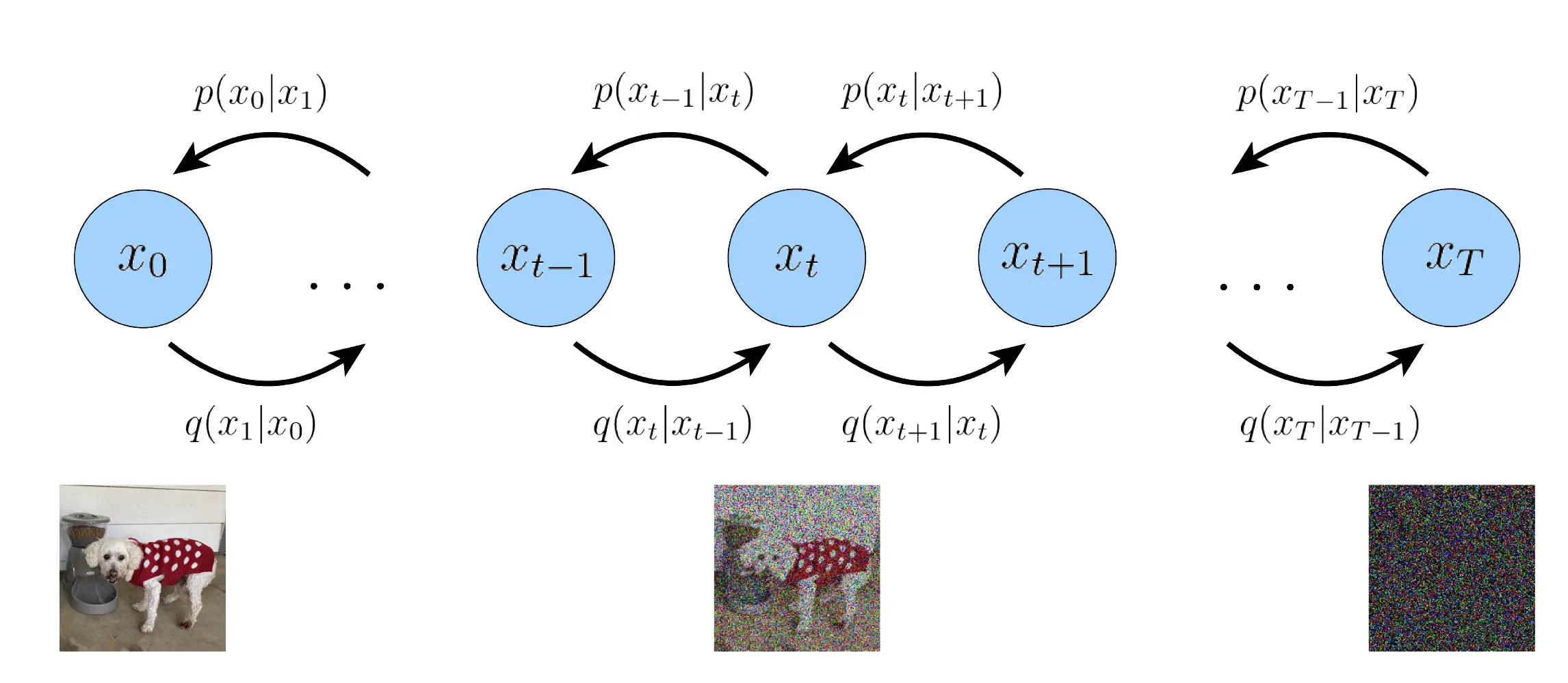
DDPM 主要包含两个处理过程,
- 一个固定/预先定义的前向扩散过程 $q$ ,选择的方法是逐渐向图像中添加高斯噪声直到最终变为纯噪声;
- 一个可学习的逆去噪扩散过程 $p_{\theta}$ , 方法是训练一个神经网络逐渐对来自纯噪声的图像去噪,指导最终获得一个真实图像;
从数据分布(某个数据集)采样一张真实图像,前向过程在每一时间步都对上一时间步的图像添加采样自高斯分布的噪声,以获得当前加噪图像。经过充分大时间步且具有较好的添加噪声的模式,最终会在有限步内(例如 $T=1000$)获得各向同性高斯分布。
数学形式
前向扩散过程
真实数据分布记为 $q(x_0)$,采样的图像表示为 $x_0\sim q(x_0)$,已知的方差模式为 $0< \beta_1 < \beta_2 < \cdots < \beta_T <1$,则前向过程定义为
$$
q(x_t|x_{t-1}) = N(x_t; \sqrt{1-\beta_t}x_{t-1},\beta_tI)
$$
时间步 $t$ 处的包含更大噪声的图像是从上一时间步 $t-1$ 加噪而来,构造的数据分布为条件高斯分布,即从该条件高斯分布中采样得到。条件高斯分布的参数为,$\mu_t = \sqrt{1-\beta_t}x_{t-1}, \sigma_t^2 = \beta_t$。
- 条件性:$x_t$ 的获取需要以 $x_{t-1}$ 为条件,或者说缩放 $x_{t-1}$ 均值变换得到;
- $\beta_t$:可以理解为缩放系数,对每一时间步而言,因此对应下标为 $t$,并且其是变化的,所谓的 “variance schedule” 表示其可以是线性、二次、余弦形式。
我们知道对一个非标准正态分布 $x\sim N(\mu, \sigma^2)$,其标准化对应的公式为 $z=\frac{x-\mu}{\sigma}\sim N(0, 1)$ 可以将其转变为标准正态分布。因此我们易得,$x$ 对应的变换公式为 $x = \mu + \sigma z$
因此,我们可以在每一时间步通过采样 $\epsilon\sim N(0, I)$ 然后表示
$$
x_t = \sqrt{1-\beta_t}{x_{t-1}} + \sqrt{\beta_t}\epsilon
$$
逆扩散过程
相对于前向扩散过程,如果我们知道 $p(x_{t-1}|x_t)$ ,则可以对 $x_T$ 随机采样出高斯噪声,然后逐渐去噪直到它变化为来自于真实数据分布的一个样本 $x_0$;
- $p(x_{t-1}|x_t)$ 的不可知性
当然,如果我们知道了这个条件概率分布,那么就很容易从纯噪声生成想要的数据样本,但是这需要知道所有可能图像的分布去计算这样的条件概率。
- $q(x_{t}|x_{t-1})$ 的可知性
之所以在这里分析前向扩散就是为了与逆向扩散进行对比,$q(x_{t}|x_{t-1})$ 是我们通过前面分析的高斯分布建立模型的,并且高斯模型的均值、协方差矩阵都是与设定的超参数相关,是固定/预先设置的过程,用于将采样的真实数据逐步变化纯噪声。因此,它是可知的,有确定性模型(参数确定)的。
- $p(x_{t-1}|x_t)$ 的参数估计
我们无法对 $p(x_{t-1}|x_t)$ 直接建立确定性的模型,但是可以利用神经网络去估计这个条件概率分布,记为 $p_{\theta}(x_{t-1}|x_t)$,这个过程中参数 $\theta$ 是可学习的,通过随机梯度下降法进行优化。
类比前向扩散过程,很容易想到逆扩散过程可能也会是一个高斯模型,含有待估计的均值、协方差参数,即
$$
p_{\theta}(x_{t-1}|x_t) = N(x_{t-1};\mu_{\theta}(x_t,t),\Sigma
_{\theta}(x_t,t))
$$
其中,对应的均值 $\mu_{\theta}$、协方差 $\Sigma_{\theta}$ 均与上一步图像样本 $x_t$ 以及当前噪声水平 $t$ 相关。
- 参数学习
正常来讲,神经网络应当学习均值 $\mu_{\theta}$ 和协方差 $\Sigma_{\theta}$ 才能实现最好的结果,事实也是如此 Improved diffusion models。但是DDPM 只学习了条件概率分布的均值而保持方差固定,即设定 $\sigma_t^2 = \beta_t$.
目标函数
$q$ 和 $p_{\theta}$ 可以被看作一个变分自动编码器(VAE),其中 variational lower bound 被用来最小化负对数似然值相对于 ground truth. 因此在每一时间步,损失函数是各时间步的损失项之和,即
$$
L = L_0 + L_1 + \cdots + L_T
$$
除了 $L_0$ 损失函数的每一项均是两个高斯分布的 KL 散度,用于度量前向扩散过程和逆向扩散过程中每一时间步对应的高斯分布的差异,实际上就是在让逆向扩散过程学习前向扩散过程。DDPM(逆扩散过程中协方差固定)中可以明确地表示为相对于均值的 L2 损失。
Nice Property
前向扩散过程的构造一个最好的特性是可以直接根据 $x_0$ 计算任意噪声水平下的样本 $x_t$,
$$
q(x_t|x_0)=N(x_t;\sqrt{\overline{\alpha_t}}x_0,(1-\overline{\alpha_t})I)
$$
其中,$\alpha_t:=1-\beta_t$ 且 $\overline{\alpha_t}:=\prod_{s=1}^t\alpha_s$
不妨表示 $x_t$, $x_{t-1}$ 如下,
$$
\begin{align*}x_{t} &= \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}\epsilon_t\newline
x_{t-1} &= \sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}\epsilon_{t-1}\end{align*}
$$
故
$$
\begin{align*}x_{t} &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}\epsilon_{t-1})+\sqrt{1-\alpha_t}\epsilon_t\newline&=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\epsilon_{t-1}+\sqrt{1-\alpha_t}\epsilon_t\end{align*}
$$
对于 $\sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\epsilon_{t-1}$ 可以将其看作一个高斯分布,其满足
$$
\begin{align*}z_1&=0+\sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\epsilon_{t-1}\newline&\sim N(0,\alpha_t(1-\alpha_{t-1})I)\end{align*}
$$
同理,对于 $\sqrt{1-\alpha_t}\epsilon_t$ 可以表示为
$$
\begin{align*}z_2&=0+\sqrt{1-\alpha_{t}}\epsilon_{t}\newline&\sim N(0,(1-\alpha_{t})I)\end{align*}
$$
对于两个相互独立的正态随机变量 $z_1\sim N(\mu_1,\sigma^2_1)$ 以及 $z_2\sim N(\mu_2,\sigma^2_2)$有 $DZ = DZ_1 + DZ_2 + 2Cov(Z_1, Z_2)=\sigma_1^2 + \sigma_2^2$
因此,$z=z_1+z_2\sim N(0,(1-\alpha_t\alpha_{t-1})I)$ 则可推得
$$
\begin{aligned}
x_{t} &=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\epsilon_{t-1}+\sqrt{1-\alpha_t}\epsilon_t\newline
&=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}\epsilon_t\newline
&=\cdots\newline
&=\sqrt{\alpha_t\alpha_{t-1}\cdots\alpha_1}x_0+\sqrt{1-\alpha_t\alpha_{t-1}\cdots\alpha_1}\epsilon_t\newline
&=\sqrt{\overline{\alpha_t}}x_0+\sqrt{1-\overline{\alpha_t}}\epsilon_t
\end{aligned}
$$
其中,记 $\alpha_t:=1-\beta_t$ 且 $\overline{\alpha_t}:=\prod_{s=1}^t\alpha_s$ .
所以,根据以上推导,可以得到直接由初始真实数据样本在噪声水平 $t$ 下的条件概率分布为
$$
q(x_t|x_0)=N(x_t;\sqrt{\overline{\alpha_t}}x_0,(1-\overline{\alpha_t})I)
$$
由以下公式可以直接看出
$$
\begin{align*}x_{t} &=\sqrt{\overline{\alpha_t}}x_0+\sqrt{1-\overline{\alpha_t}}\epsilon_t\end{align*}
$$
这种特性可以解释为,从高斯噪声中采样 $\epsilon_t$,将它添加到真实样本 $x_0$ 中并通过适当缩放 $\overline{\alpha_t}$ 可以直接得到 $x_t$。由于 $\overline{\alpha_t}$ 可以预先计算,这启示我们,在训练过程中,可以优化损失函数 $L$ 的随机项 $L_t (t=1\cdots T)$,整个优化过程变为采样时间步 $t$,采样高斯噪声 $\epsilon_t$,优化 $L_t$.
Noise Predictor
由于前面推到的优美的特性,可以使得参数化均值后的神经网络去学习添加的噪声($\epsilon_\theta(x_t, t)$) 而不是学习均值,因为从 $x_0$ 直接推导到 $x_t$ 对应的均值并不是在时间步 $t$ 由上一时间步 $t-1$ 推导的均值,而为了避免重复计算 $q$ 过程来获得 $x_t$,显然利用上述特性是最好的方式。
而损失函数的计算就转化为衡量添加噪声与预测噪声之间的差异。均值可以通过以下公式计算得到
$$
\mu_{\theta}(x_t,t)=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\overline{\alpha_t}}}\epsilon_{\theta}(x_t,t))
$$
Loss Function
最终的目标函数 $L_t$ 表示为
$$
||\epsilon-\epsilon_\theta(x_t,t)||^2 = ||\epsilon-\epsilon_\theta(\sqrt{\overline{\alpha_t}}x_0+\sqrt{(1-\overline{\alpha_t})}\epsilon,t)||^2
$$
其中,$\epsilon\sim N(0, I)$ 表示在时间步 $t$ 采样的纯噪声,$\epsilon_\theta(x_t,t)$ 表示构建的神经网络,噪声预测采用 MSE 计算损失。
训练流程

- 从真实数据分布 $q(x_0)$ 中随机采样 $x_0$;
- 从 $1\sim T$ 中均匀随机采样噪声水平/时间步 $t$;
- 从高斯分布中随机采样噪声 $\epsilon$ , 并将其直接应用于 $x_0$ 获得 $x_t$;
- 神经网络基于给定的当前时间步样本 $x_t$ 预测添加的噪声;
- 计算采样噪声 $\epsilon$ 与预测的噪声 $\epsilon_\theta$ 之间的损失,更新模型参数;
Reference
Deep Into Denoising Diffusion Probabilistic Models (DDPM)