Instant-NGP | SIGGRAPH 2022 | Paper Reading
Instant Neural Graphics Primitives with a Multiresolution Hash Encoding
工作类型(首次/改进) 技术路线 创新点 日期 首次 MLP, Hash Coding 多分辨率哈希编码 2025-03-27
文章摘要
用全连接神经网络表示的神经图形原语具有高昂的训练和评估成本。作者提出了一个多功能输入编码策略能够允许使用更小的神经网络而不牺牲质量,因此明细地减少了浮点运算和内存访问次数。
较小的神经网络是通过一个具有可训练特征向量的多分辨率哈希表进行增强的,而且这种多分辨率结构允许网络消除哈希冲突,使得其变成一个简单的结构能够在现代GPUs上轻松实现并行化。该方法能够实现几个数量级的加速,在几秒钟之内就可以实现高质量神经图元的训练并在数十毫秒内完成$1920\times 1080$分辨率图像的渲染。
核心贡献
- 作者提出了一个使用多分辨率哈希编码的即时神经图元,能够允许使用更小的神经网络而不牺牲质量,因此明细地减少了浮点运算和内存访问次数。
研究背景
在计算机图形中,我们需要参数化的数学函数用以表示形状和场景发光等信息,这些函数需要既准确又高效。基于多层感知器(MLPs)的神经网络表示已经显示出具有高视觉质量和紧凑性。尽管如此,这些方法往往依赖于特征图结构和历时性的训练方法,且在大型近似需要时质量会大幅下降。该研究正是要克服这种方法的局限性。
研究动机
在以往的自注意力架构 (Recurrent Architecture)和自注意力网络 (Transformer)中,通过加权的方式来处理包括相对位置的学习活动。而在此之前,同样是编码工作,对于输入变量并将其标示成更控制的线性分离标签的工作也作出了巨大的贡献。此工作填充输入编码技术自身结合常见的数据结构化,并且以多分辨率哈希技术达到高效率、低空间存储等方面的效率优化。
技术方法
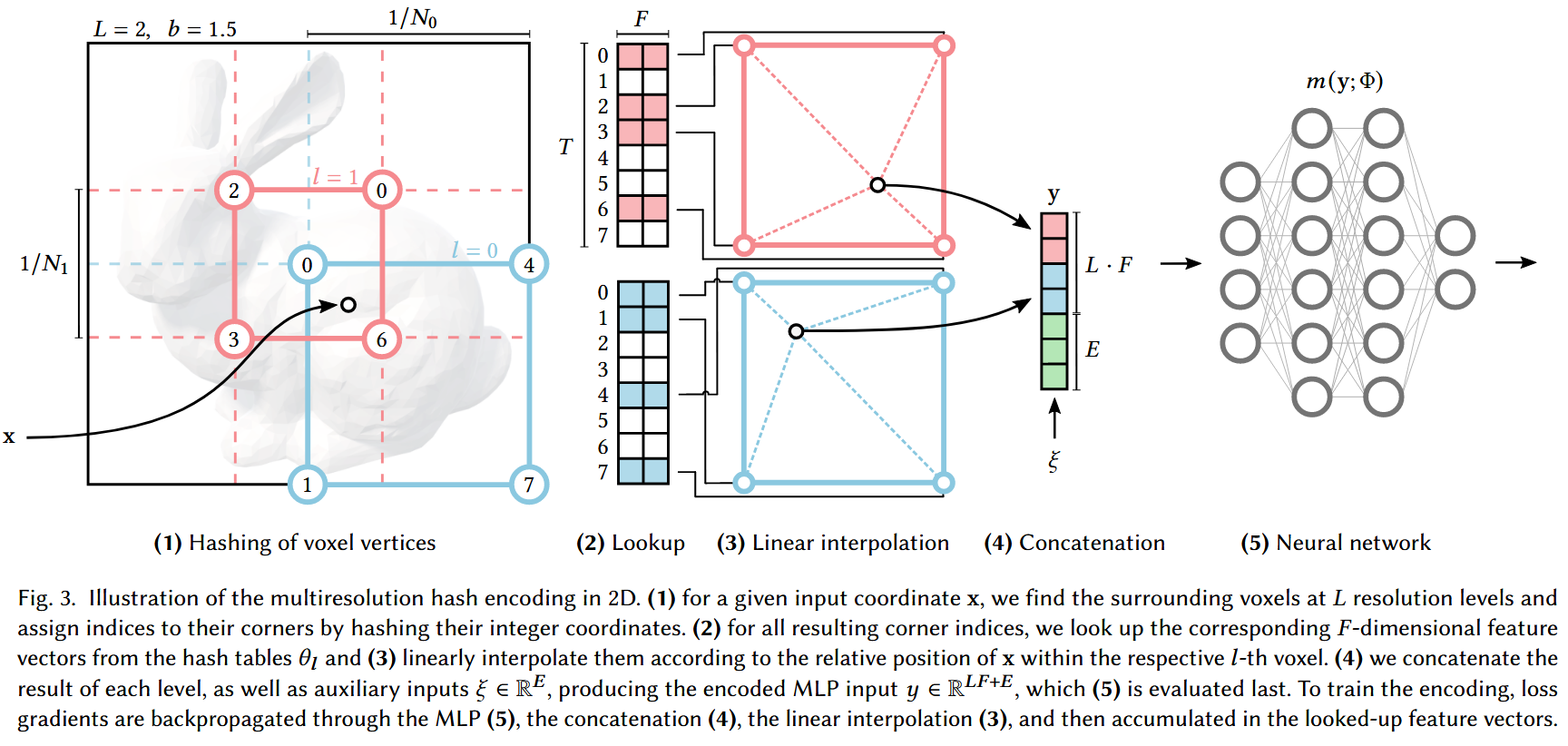
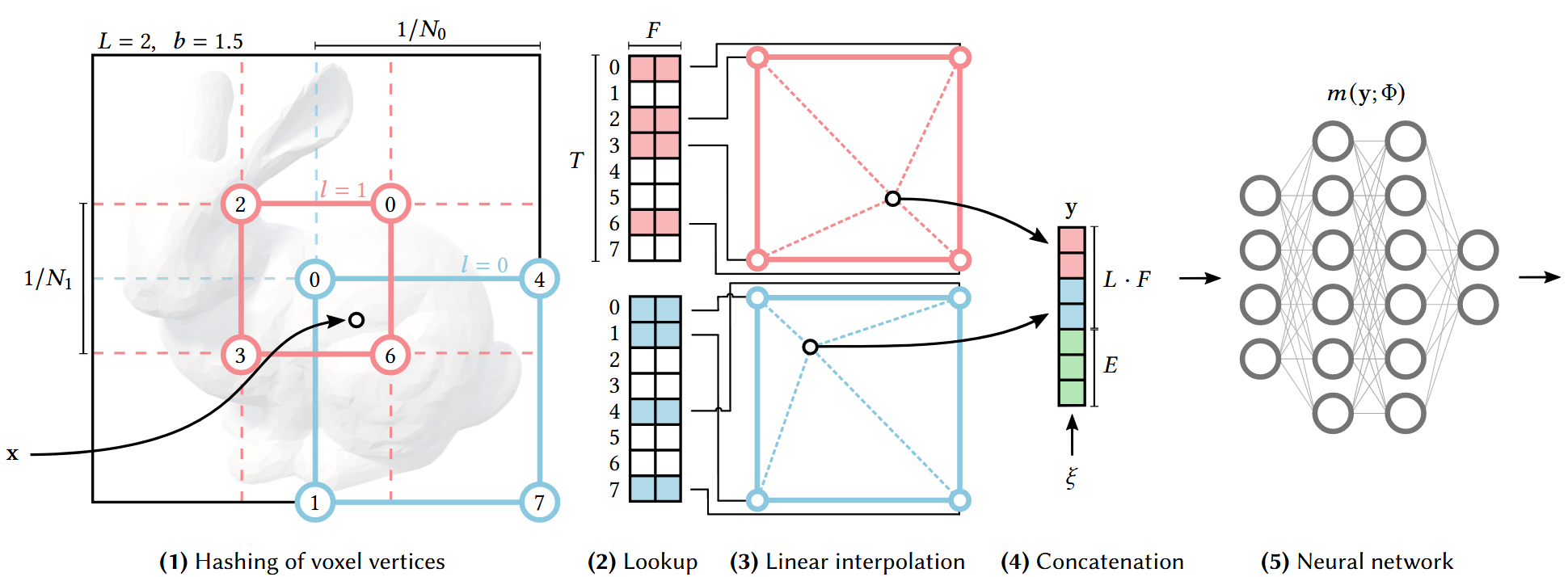
粗细网格分辨率
在多分辨率网格中,采取从粗到细的采样策略,设置最粗略的分辨率为 $N_{\text{min}}=16$ ,最细致的分辨率为 $N_{\text{max}}\in [512, 524288]$ 因为最高的分辨率就是每一个像素作为一个单元,但是这会加重存储以及运算负担。因此,作者设置最高分辨率作为一个参数进行学习,以找到性能与质量的平衡点。
当设定最粗和最细的分辨率后,中间的多级分辨率采取等比级数的方式进行确定,因此第 $l$ 层网格分辨率可以通过以下公式获取。
$$
N_l := \lfloor N_{\text{min}}\cdot b^l\rfloor \tag{1}
$$
$$
b:= \exp(\frac{\ln N_{\text{max}}-\ln N_{\text{min}}}{L-1})
\tag{2}
$$
其中,$L$ 表示分辨率网格级数,$b\in[1.26, 2]$ 是估计出的等比系数。
至于在图(1)中网格中每一个小单元边长是 $1/N_0, 1/N_1$,是因为网格分辨率为 $N_l\times N_l$ 而通过归一化后的NDC空间维度是 $[-1, 1]^3$,因此需要除以分辨率得到每一个小格的长度。
哈希体素顶点
对单个分辨率水平 $l$ ,输入的坐标为 $\boldsymbol{x}\in \mathcal{R}^d$,$d$ 表示坐标空间的维度。通过对该点坐标进行向上和向下取整来确定所在该分辨率网格的体素。
$$
\lfloor\boldsymbol{x}_l\rfloor := \lfloor\boldsymbol{x}\cdot N_l\rfloor, \lceil\boldsymbol{x}_l\rceil := \lceil\boldsymbol{x}\cdot N_l\rceil\tag{3}
$$
由于 $\boldsymbol{x}\in[0, 1]$ 乘以分辨率并取整,就是在对NDC空间进行光栅化以形成像素空间,只不过这里考虑的是三维空间,即称作体素空间。
在论文中,称 $\lfloor\boldsymbol{x}_l\rfloor, \lceil\boldsymbol{x}_l\rceil$ 包围的体素空间具有 $2^d$ 个顶点,这是因为统一了 $d>3$ 的情况。但实际上,可以认为在三维空间中,$d=3$ 也即所在的体素有8个顶点。
分辨率为 $N_l\times N_l$ 的网格有 $(N_l+1)^d$ 个体素顶点,可以证明:
不妨设 $d = 3$,即在3维空间中,整个 NDC 空间在该分辨率网格光栅化后,每一个坐标轴上都有 $(N_l+1)$ 个顶点,范围为:
$$
(0, \frac{1}{N_l}, \frac{2}{N_l},\cdots, \frac{N_l-1}{N_l}, 1)\tag{4}
$$
那么,任意一个点的坐标表示为,$(0,0,0)\rightarrow (1, 1, 1)$,每一个维度都有$(N_l+1)$ 种选择,由组合定律可得,所有的不重复点坐标有 $N$ 个,
$$
N = C_{N_l+1}^1\cdot C_{N_l+1}^1\cdot C_{N_l+1}^1 = (N_l+1)^3\tag{5}
$$
因此,对于 $d$ 维空间,对应的所有体素顶点有 $(N_l+1)^d$ 个。
每一个分辨率网格具有固定的哈希表大小 $T$,这是需要进一步学习的参数,每个体素顶点都被映射为哈希表的一项,表示为 $F=2$ 维的可学习特征向量。映射的关系实质上就是三维矩阵坐标转换为顺序排列数组下标的过程。
当 $(N_l+1)^d\leq T$ 时,这种哈希映射关系将会是 1:1 而不会发生哈希冲突问题,但是当遇到更细粒度的分辨率网格时,需要使用一个哈希函数尽可能避免冲突,即 $h: \mathcal{Z}^d\rightarrow \mathcal{Z}_T$.
$$
h(\boldsymbol{x}) = (\bigoplus^d_{i=1}x_i\pi_i)\mod T\tag{6}
$$
其中,$\bigoplus$ 表示逐位异或操作,$\pi_i$ 是一个独特的大素数,选取的策略是 $\pi_1:=1, \pi_2:=2 654 435 761,\pi_3 := 805 459 861$。
线性插值
当通过坐标点找到每一个分辨率体素网格中的8个顶点后,可以在哈希表中查找出对应的特征向量。
随即,根据坐标点距离体素顶点的相对距离,进行三线性插值操作,得到每一个分辨率网格下提取出的坐标点特征向量。
三线性插值基本思想
假设我们有一个规则的三维网格,其中每个网格点存储一个标量值 $f(x,y,z)$。我们希望在网格点之间的某个非网格点 $(x, y, z)$ 估计其对应的值。
在三维空间中,每个查询点被包含在一个立方体中,该立方体由 8 个最近的网格点围成。三线性插值的基本思路是:
- 先在 X 方向进行线性插值,得到 4 个中间值。
- 再在 Y 方向进行线性插值,得到 2 个中间值。
- 最后在 Z 方向进行线性插值,得到最终插值结果。
拼接
拼接所有层次分辨率网格提取的特征向量,以及引入的额外辅助输入 $\xi \in \mathcal{R}^E$,例如编码的视角以及辐射场的纹理,最终获得编码后的输入特征 $\boldsymbol{y}\in \mathcal{R}^{LF+E}$。
定量结果
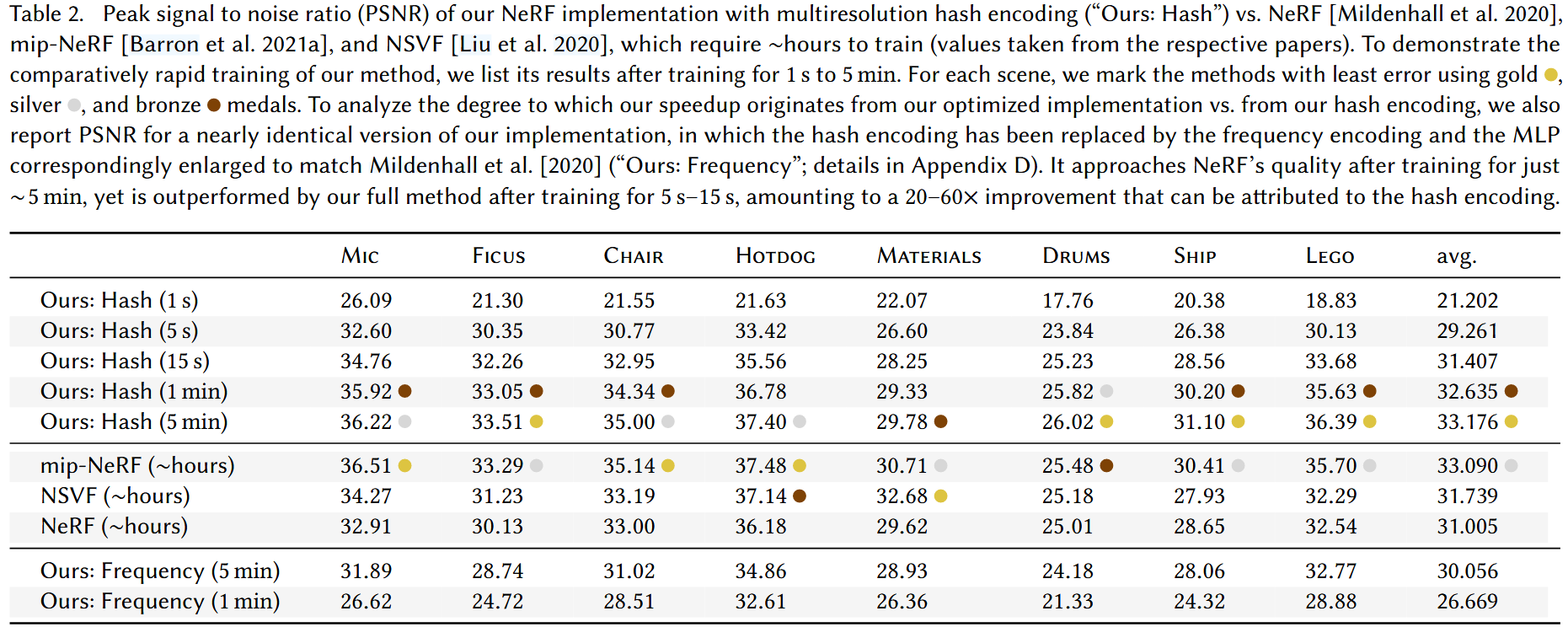
参考文献
- Müller et al. (2022). Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. arXiv SIGGRAPH arXiv:2201.05989.
Instant-NGP | SIGGRAPH 2022 | Paper Reading