RAD-NeRF | 2022 | Paper Reading
Real-time Neural Radiance Talking Portrait Synthesis via Audio-spatial Decomposition
工作类型(首次/改进) 技术路线 创新点 日期 首次 Efficient NeRF, MLP 音频特征空间分解 2025-03-26
文章摘要
Dynamic NeRF 在talking portrait 上面实现了很大成功,但是仍存在训练速度以及推理速度缓慢的问题。本文利用 grid-based NeRF 提出了一个高效地 NeRF-based 框架——Realtime Audio-spatial Decomposed NeRF (RAD-NeRF),能够实现实时 talking portiait 合成以及快速收敛。
核心贡献
- 作者提出了一个 Decomposed Audio-spatial Encoding Module,实现用两个低维的特征网格(一个3D空间网格和一个2D音频网格)建模内在的高维audio-driven facial dynamics。
- 作者提出了一个轻量化的 Pseudo-3D Deformable Module 能够进一步增强合成与头部运动同步的躯干运动的高效性。
- RAD-NeRF 相比于之前的方法能够实现 500 倍的加速同时保证更好的渲染质量,而且还支持各种talking portrait 的显示控制(head pose, eye blink, and background image)。
研究背景
Audio-driven Talking Portrait Synthesis
这个方向的任务对于给定一个任意输入的音频,重演(reenact)一个指定的人。重演(reenact)通常指的是利用输入的语音信号来驱动一个静态肖像或参考视频中的人物,实现其面部表情、唇形运动、头部姿态等动态表现的重现。
Conventional Methods
传统方法通常定义一组音素与嘴型的对应规则,并采用基于拼接(stitching-based)的技术来修改嘴型。
Deep Learning Based
深度学习一般是基于2D图像的研究方法,旨在合成与音频输入对应的图像。
具有的劣势便在于,只能生成固定分辨率的图像而且不能够控制头部姿势(因为是直接生成图像)。
Model Based
基于模型的一类方法主要采用结构化表示(facial landmarks and 3D morphable face models)来帮助 talking portrait 合成。
面临的问题是,中间表示的估计可能会引入额外的误差。
NeRF Based
NeRF 是利用隐式神经辐射场进行重建的方法,能够以任意分辨率实现photorealistic rendering并且仅需要更少的数据。
对应的问题是,由于使用极为复杂的 MLP 网络,导致缓慢的训练速度以及推理速度。
Neural Radiance Field
神经辐射场结合了隐式神经表示与体积渲染进行新颖视图合成。最近的研究热点关注于动态场景建模(Dynamic Modeling)以及高效神经表示(Efficient Nerual Representation)。
Dynamic Modeling
动态场景建模分为两类,一类是基于形变的方法(Deformation-based),旨在通过学习一个形变场将所有观测值映射回到一个标准空间,然后与原有的参数值进行叠加。
另外一类则是,基于调制的方法(Modulation-based),将表示时间或音频的特征作为 NeRF 的输入,直接学习视锥函数(plenoptic function)。
- Deformation-based 方法通过显式学习变形场来捕捉动态变化,具有较好的几何解释性,但在处理大幅度或复杂变形时可能存在局限性;
- Modulation-based 方法直接将时间条件化,模型结构较为简洁并且具有较强的适应性,但缺乏对运动的直观解释,同时对网络容量的要求较高。核心优势在于能够更好地建模复杂动态变化,尤其是拓扑结构的改变,因此更加适合建模人脸动态变化。
Efficient Nerual Representation
原始的NeRF(vanilla NeRF) 以及后续工作通常使用一个 MLP 编码 3D 场景,这种隐式 NeRF 由于在渲染一张图象时,需要在所有采样坐标处执行大量的评估,往往会导致缓慢的训练和推理速度。因此,许多针对性的加速工作也逐渐兴起。
最近的加速的研究工作提出,减小 MLP 的大小或者完全移除它然后使用显示 3D 特征网格结构储存 3D 场景特征。
- DVGO 直接使用一个密集特征网格用于加速;
- Instant-NGP 采用一个多分辨哈希表以控制模型大小;
- TensoRF 分解密集的 3D 特征网格为紧凑的低秩张量。
研究动机
Talking Portrait Synthesis 领域需要实现实时渲染的要求,而针对 NeRF 加速的 Grid-based NeRF 类方法只适用于静态场景,现有应用这些加速方法到 Dynamic NeRF 的工作要么是基于形变的(之前分析,该类方法不能够应对大幅度以及复杂变化),要么是只支持时间依赖性的。
因此,需要将 Grid-based NeRF 加速方法迁移到 audio-driven setting 中,实现音频依赖性的 talking portrait synthesis。
技术方法
NeRF
给定采样点的坐标以及射线方向,学习隐式函数来表示对应点的体密度 $\sigma$ 以及RGB颜色 $\boldsymbol{c}$,如下公式所示。
$$
\begin{align}
F:\boldsymbol{x}, \boldsymbol{d} \longrightarrow\sigma,\boldsymbol{c}\tag{1}
\end{align}
$$
其中,$\boldsymbol{x} =(x,y,z)$ 表示采样点的位置坐标, $\boldsymbol{d} = (\theta, \phi)$ 表示球面坐标系下的方向角,如下图所示,与高等数学中的类似,只是在此去掉了半径 $r$ 因为不需要考虑球面,而是考虑的采样点,通过位置坐标 $\boldsymbol{x}$ 代替了,并且 $\theta$ 称为极角,这和极坐标系保持一致;$\phi$ 称为方位角,主要用来判断纬度方向。

射线表示
射线有一个端点以及指定的方向构成,因此给定相机中心坐标 $\boldsymbol{o}\in \mathcal{R}^3$,光线的方向 $\boldsymbol{d}=(\theta, \phi) = (\sin\theta\cos\phi, \sin\theta\sin\phi, \cos\theta)\in\mathcal{R}^3$,在计算最终的射线时,坐标以及方向要统一转换到一种坐标系下,在这里将球面坐标系方向向量转换为直角坐标系下的方向向量,而且是单位方向向量。由于相机模型中,坐标系跟现在的坐标系设置不一致,此处仅为了探究,具体到应用再进行转换即可。
给定一个缩放系数,或者说是指定的距离,就可以表示一条任意的射线,不妨令 $t\in \mathcal{R}, t>0$ ,
$$
\boldsymbol{r} = \boldsymbol{o}+t\boldsymbol{d}\tag{2}
$$
可以证明 $||t\boldsymbol{d}||_2 = \sqrt{t^2}||\boldsymbol{d}||_2=t$ 因此 $t$ 即是表示当前点 $\boldsymbol{r}$ 与中心坐标 $\boldsymbol{o}$ 的距离,当对任意的 $t$ 取任何值时,形成的点按照给定的方向 $\boldsymbol{d}$ 不断地变化,形成一条射线。
离散采样点
通过确定相机中心到某个像素的射线方向后,就可以在这条射线上进行采样,以估计处该采样点对应的体密度以及颜色值,随后便可以进行渲染出场景。
采样点的获取是通过离散化距离值 $t$ 得到的,即 $t = t_i, i=0, 1, 2, \cdots$ 对应的离散化采样点坐标为,
$$
\boldsymbol{x}_i=\boldsymbol{o}+t_i\boldsymbol{d},i=0,1,2,\cdots\tag{3}
$$
颜色混合
在获取到一系列采样点的体密度以及颜色值属性后,通过数值积分来计算得到对应像素点的RGB颜色值。对级数的积分就是级数求和,因此会根据所有点对像素点颜色的贡献度来进行混合。
$$
\boldsymbol{C}(\boldsymbol{r}) = \sum_iT_i\alpha_i\boldsymbol{c}_i\tag{4}
$$
其中,$\alpha_i=1-\exp(-\sigma_i\delta_i)$ 用于衡量单个采样点的不透明度,$\delta_i=t_{i+1}-t_i$ 表示相邻采样点之间的距离。
$\exp(-\sigma_i\delta_i)$ 表示比尔-朗伯定律(Beer-Lambert law)中光线穿过距离 $\delta_i$ 后未被吸收的透射率,可以理解为反射出光线的概率,而计算采样点的不透明度时,可以认为是光线在该步长内被吸收的概率 $1-\exp(-\sigma_i\delta_i)$。
混合所有点的不透明度时,需要考虑在该采样点前方的透射率,以此表示当前采样点在最终像素点上未被遮挡的部分。$T_i=\prod_{j<i}(1-\alpha_j)$ 即混合所有之前点的透明度即可。
最终将之前采样点的透射率(transparency),当前点的不透明度(opacity)作为权重,乘以当前点的 RGB 颜色值,即可表示当前采样点对最终像素点的贡献程度。
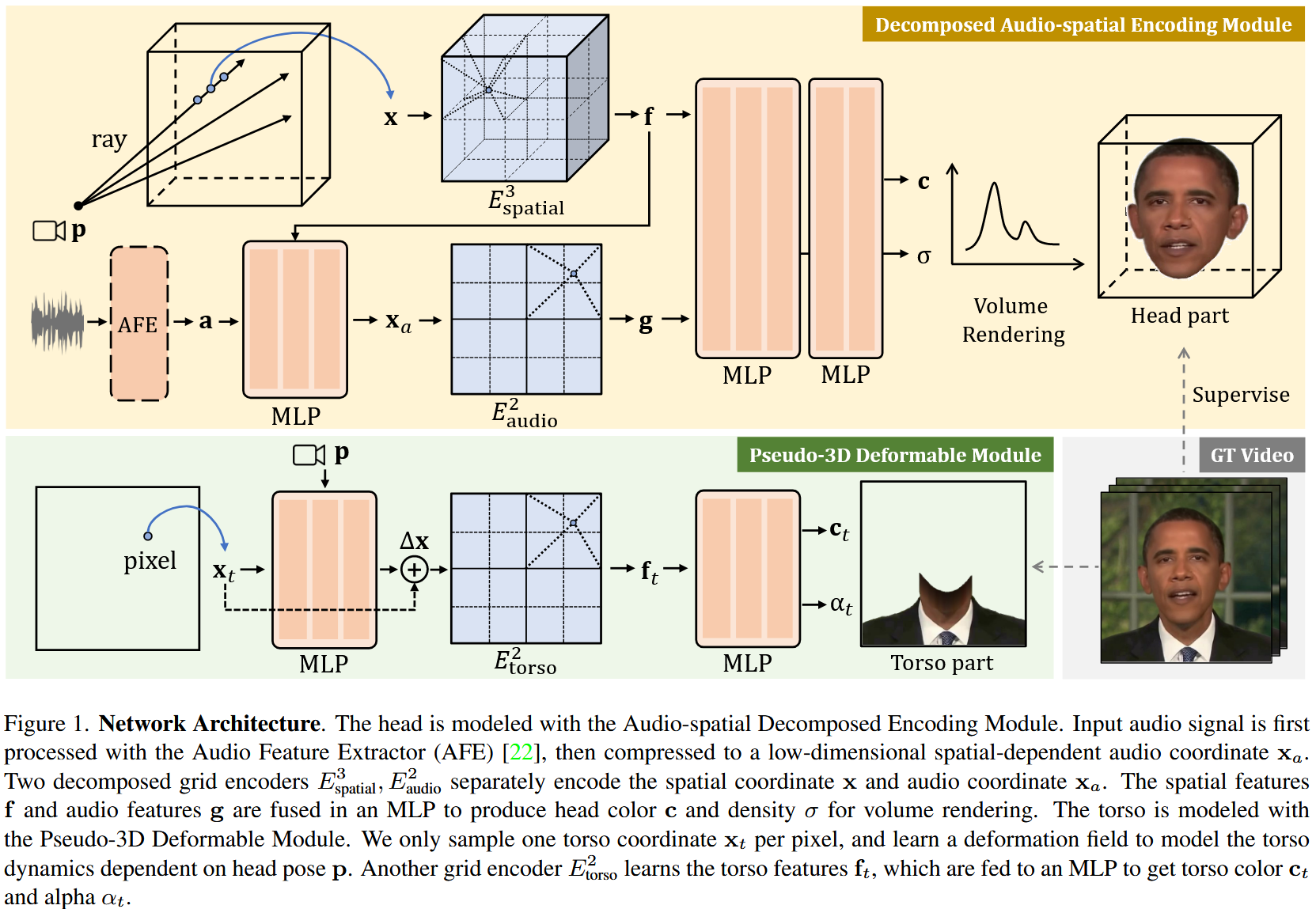
Decomposed Audio-spatial Encoding Module
Audio-spatial Encoding
音频-空间特征表示与解耦,在 RAD-NeRF 中,最重要的改进是将高维的音频特征压缩到低维空间中,实现效率上的提高。
利用 MLP 作为编码器,首先将音频从高纬特征空间中映射到低维空间中,由于维度较低,不超过三维,降维后的特征又被称作音频坐标。
$$
\boldsymbol{x}_a=\text{MLP}(\boldsymbol{a}, \boldsymbol{f})\in \mathcal{R}^D, D\in{1, 2,3}\tag{5}
$$
其中,$\boldsymbol{a}$ 表示通过AD-NeRF提取出的音频特征,$\boldsymbol{f}$ 表示通过网格编码器提取出的空间特征,拼接 $\boldsymbol{f}$ 目的在于能够显式地建模音频特征对空间位置的依赖性。
Audio-spatial Decomposition
Grid-based NeRF 类方法主要是基于 Instant-NGP 作为网格编码器将空间坐标转换为根据体素网格顶点建立起的哈希表特征,能够实现快速地特征查询。
为了进一步降低网格编码器中的线性插值复杂度,提取出的空间位置坐标和音频特征坐标解耦为两个低纬度的网格编码器分别进行编码,
$$
\boldsymbol{f} = E_{\text{spatial}}^3(\boldsymbol{x}), \boldsymbol{g}=E^3_{\text{audio}}(\boldsymbol{x_a})\tag{6}
$$
复杂度的证明
合并两个位置坐标统一编码时, $\boldsymbol{g} = E^{3+D}(\boldsymbol{x}, \boldsymbol{x}_a)$
不妨假设原结论成立
$$
2^{3+D}>2^3+2^D(D\geq 1)
$$
即
$$
\begin{align}
8\cdot2^D-2^D&>2^3\newline
2^{3-D}&<7
\end{align}
$$
当且仅当 $D\geq1$ 时成立。
Explicit Eye Control
对于眼睛的控制,主要是根据眼睛区域面积 $I_{\text{eye}}$ 占整个人脸区域面积 $I_\text{face}$ 的比例系数,简化地作为眼睛的一维度特征向量。
$$
\begin{align}
\boldsymbol{e}=100\frac{I_{\text{eye}}}{I_{\text{face}}}\in[0, 0.005]
\end{align}\tag{7}
$$
Overall Head Representation
综合以上音频、空间位置、眼睛等特征,通过 MLP 编码学习最终的RGB颜色值和体密度值。
$$
\boldsymbol{c},\sigma = \text{MLP}(\boldsymbol{f}, \boldsymbol{g}, e, \boldsymbol{i})\tag{8}
$$
其中,$\boldsymbol{i}$ 表示一个隐式外观嵌入。
Pseudo-3D Deformable Module
RAD-NeRF认为躯干部分的运动幅度不大,使用完整的动态 NeRF 能力有点过剩,因此采取了另外一个更加高效的模块。
该模块仅在图像空间中采样像素坐标 $\boldsymbol{x}_t\in\mathcal{R}^2$ 并且以头部姿势为条件 $\boldsymbol{p}$ 预测躯干部分坐标点的形变 $\Delta\boldsymbol{x} = \text{MLP}(\boldsymbol{x}_t, \boldsymbol{p})\in \mathcal{R}^2$,然后类似残差连接将原坐标与形变坐标相加,作为网格编码器的输入。
$$
\boldsymbol{f}_t=E_\text{torso}^2(\boldsymbol{x}_t+\Delta\boldsymbol{x})\tag{9}
$$
最后通过另外一个独立的MLP编码特征预测出对应的颜色值和体密度。
$$
\boldsymbol{c}_t,\alpha_t=\text{MLP}(\boldsymbol{f}_t, \boldsymbol{i}_t)\tag{10}
$$
损失函数
MSE
逐像素损失进行监督。
$$
\mathcal{L}\text{color}=\sum{\boldsymbol{c}\in I} ||\boldsymbol{c}-\boldsymbol{c_\text{gt}}||^2_2\tag{11}
$$
熵约束
促使图像中每一个像素的透射率 $\alpha$ 趋向于0或1,
$$
\mathcal{L}\text{entropy}=-\sum{\alpha\in I}(\alpha\log \alpha+(1-\alpha)\log(1-\alpha))\tag{12}
$$
L1 约束
约束非人脸区域的音频坐标模值趋向于0,避免非人脸区域受到音频影响引起意外闪烁。
$$
\mathcal{L}{\text{dynamic}}=\sum{\boldsymbol{x}_a\in\overline{I}_\text{face}}|\boldsymbol{x}_a|\tag{13}
$$
其中,$\overline{I}_\text{face}$ 表示非人脸区域,目的时对应的 $\boldsymbol{x}_a$ 趋向于 0。
LIP 微调
单独优化嘴唇区域,采取MSE结合结构损失函数 LPIPS。
$$
\mathcal{L}{\text{fine-tune}}=\sum{\boldsymbol{C}\in \mathcal{P}}||\boldsymbol{C}-\boldsymbol{C}_\text{gt}||^2_2+\lambda\text{LPIPS}(\mathcal{P}, \mathcal{P}_\text{gt})\tag{14}
$$
其中,$\mathcal{P}$ 表示嘴唇(LIP)区域,是图像当中的一小块。
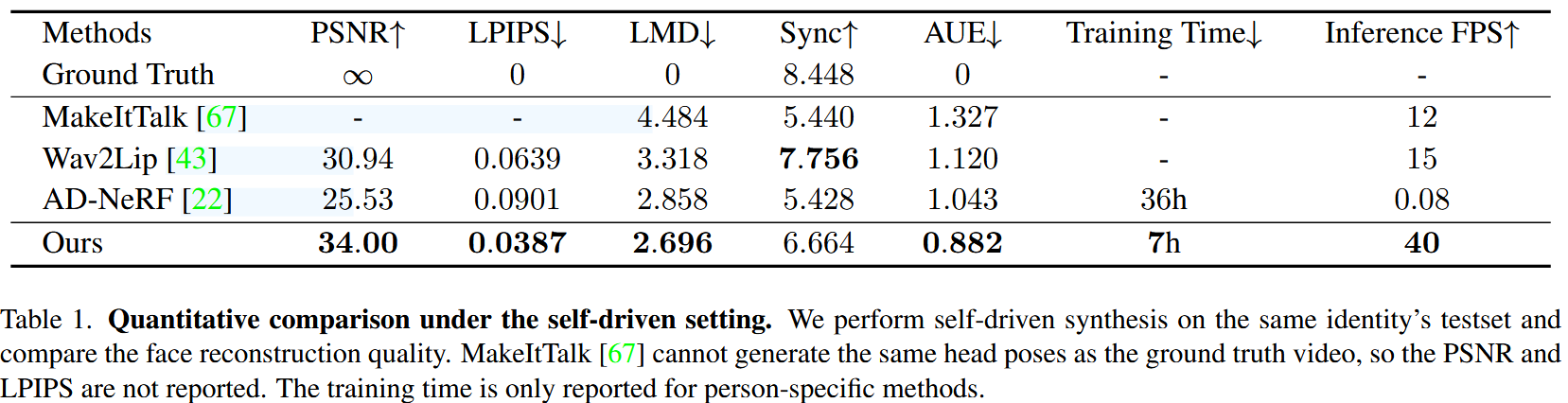
定量结果
参考文献
- Tang et al. (2022). Real-time Neural Radiance Talking Portrait Synthesis via Audio-spatial Decomposition. arXiv preprint arXiv:2211.12368.
RAD-NeRF | 2022 | Paper Reading